[알고리즘] 병합 정렬(Merge Sort) vs 퀵 정렬(Quick Sort)

병합 정렬(Merge Sort)과 퀵 정렬(Quick Sort)에 대해서 알아보자
안녕하세요 👀 오늘은 알고리즘 중에서 정렬할때 쓰이는 대표적인 알고리즘 두 가지를 알아볼게요!
정렬 알고리즘은 컴퓨터 과학에서 매우 중요한 개념이죠. 특히, 대용량 데이터를 효율적으로 정렬하는 것은 아주아주 중요한데요. 이번 포스팅에서는 두 가지 주요 정렬 알고리즘인 병합 정렬(Merge Sort)과 퀵 정렬(Quick Sort)에 대해 알아볼겁니당. 각 알고리즘에 대해 자세히 알아보고 시간복잡도까지 알아보도록 합시당
🍊 병합 정렬(Merge Sort)이란?
병합 정렬은 분할 정복(Divide and Conquer) 방식을 사용하여 작동하는 정렬 알고리즘입니다.
이 알고리즘은 큰 문제를 작은 문제로 나누어(divide) 해결하며, 나중에 작은 문제의 해답을 하나씩 결합하여(conquer) 원래의 문제를 해결합니다. 제가 좋아하는 수학자 존 폰 노이만이 1945년에 개발한 알고리즘이에요 🙃
🙋🏻♀️ 분할 정복? 그게 뭔데요
분할-정복 알고리즘은 divde and conquer 라고 해서 문제를 나눌 수 없을 때까지 나누어서 각각을 풀면서 다시 합병하여 문제의 답을 얻는 알고리즘입니다. 더 자세히 알고 싶으면 이 포스팅을 참고해 주세요
📍merge sort의 동작 원리

위 그림을 보면 아시겠지만, 실제 "정렬" 과정은 결합(conquer)할 때 이루어집니다.
📍merge sort의 시간복잡도
- Best-case: O(nlog(n))
- Average-case: O(nlog(n))
- Worst-case: O(nlog(n))
📍merge sort를 자바스크립트로 구현해보자
// 정렬된 left, right 배열을 하나로 합치는 merge 함수
function merge(left, right) {
// left, right 배열은 이미 정렬되어 있다.
const result = [];
while (left.length !== 0 && right.length !== 0) {
left[0] <= right[0] ? result.push(left.shift()) : result.push(right.shift());
}
return [...result, ...left, ...right];
}
function mergeSort(array) {
// array 요소가 하나가 남을 때 재귀 종료
if (array.length === 1) return array;
// 2로 나누고 내림을 해야 length 가 2일 때도 안전하게 배열을 slice 할 수 있다.
const middleIndex = Math.floor(array.length / 2);
const left = array.slice(0, middleIndex);
const right = array.slice(middleIndex);
// 재귀로 계속해서 반으로 나누면서 length 가 1이 될때까지 쪼개고,
// 거꾸로 올라오면서 순수한 함수인 merge에 인자로 넣어서 다시 병합되어서 최종값을 리턴한다.
return merge(mergeSort(left), mergeSort(right));
}
const arr = [4, -1, 0, -8, 0, 8, 91, 2, 3, 4, 98, 911, 21];
const result = mergeSort(arr);
console.log("result: ", result);
// result: [ -8, -1, 0, 0, 2, 3, 4, 4, 8, 21, 91, 98, 911 ]
🍊 퀵 정렬(Quick Sort)이란?
quick sort 또한 merge sort와 마찬가지로 분할-정복 알고리즘을 기반으로 이루어진 정렬 알고리즘입니다. 다른 점이 있다면, quick sort는 피벗(pivot)이라는 기준이 되는 요소를 이용해서 정렬한다는 것입니다.
아래는 quick sort가 이루어지는 과정입니다.
📍 quick sort의 동작 원리
1. pivot을 고릅니다.
가장 오른쪽 요소를 고르고 이것을 피벗(pivot)이라고 부릅니다.

2. 배열을 재정렬합니다.
pivot을 기준으로 재정렬합니다.
그러니까 pivot보다 작은 요소들은 pivot의 왼쪽으로 가도록, pivot보다 큰 요소들은 오른쪽으로 가도록 합니다.

3. pivot을 기준으로 배열을 나눕니다.
정렬된 후 pivot을 기준으로 다시 나뉘어진 두 배열은 각각 또 pivot을 선택합니다. 그리고 2번의 과정을 다시 반복합니다.
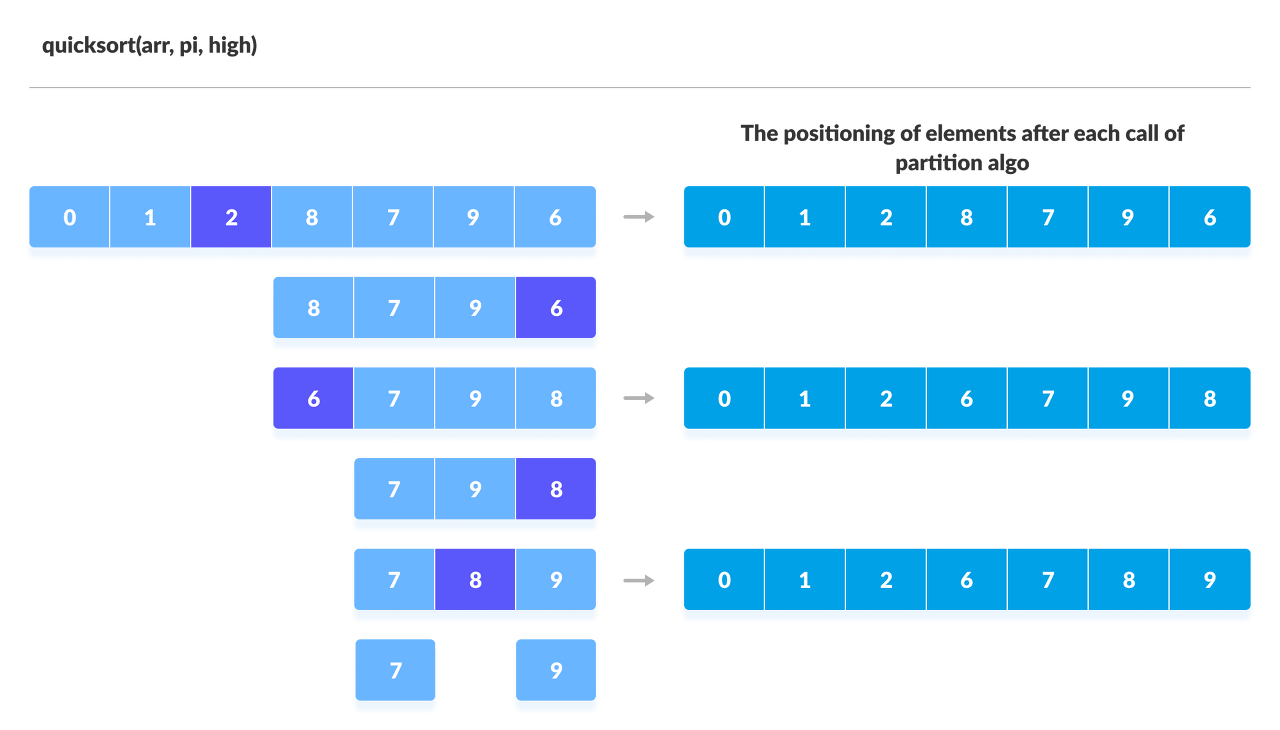
1~3번의 과정이 나뉘어진 각 배열의 요소가 하나씩 남을 때까지 반복합니다.

📍quick sort의 시간복잡도
- Best-case: O(n*log(n))
- Average-case: O(n2)
- Worst-case: O(n*log(n))
📍quick sort를 자바스크립트로 구현해보자
function quickSort (array) {
if (array.length < 2) {
return array;
}
const pivot = [array[0]];
const left = [];
const right = [];
for (let i = 1; i < array.length; i++) {
if (array[i] < pivot) {
left.push(array[i]);
} else if (array[i] > pivot) {
right.push(array[i]);
} else {
pivot.push(array[i]);
}
}
console.log(`left: ${left}, pivot: ${pivot}, right: ${right}`);
return quickSort(left).concat(pivot, quickSort(right));
}
const sorted = quickSort([5, 3, 7, 1, 9]);
console.log(sorted);
🍊 결론
퀵 정렬과 병합 정렬은 모두 효율적인 정렬 알고리즘으로 알려져 있습니다. 각각의 알고리즘은 분할 정복 알고리즘의 원리를 활용하여 입력 리스트를 분할하고 정렬하며 결합합니다.
퀵 정렬은 평균적으로 매우 빠른 실행 속도를 가지고 있으며, 특히 큰 데이터 집합을 정렬할 때 효과적입니다. 그러나 최악의 경우에는 성능 저하가 발생할 수 있으므로 기준점(pivot)의 선택에 주의해야 합니다. 반면, 병합 정렬은 안정적인 정렬 알고리즘이며, 평균 및 최악 시간 복잡도가 O(nlogn)으로 매우 효율적입니다. 추가적인 메모리 공간을 사용하나 안정성과 효율성을 보장합니다.
따라서, 퀵 정렬과 병합 정렬은 각자의 특징과 장단점을 가지고 있으며, 주어진 상황과 요구사항에 맞는 알고리즘을 선택하여 적재적소에 사용하면 되겠습니다 👍🏻
참고 자료
Merge Sort - JavaScript
In this article we'll go through Merge Sort step-by-step, implement Merge Sort in JavaScript, discuss Merge Sort performance and the advantages and disadvantages of Merge Sort.
www.doabledanny.com
QuickSort (With Code in Python/C++/Java/C)
Quicksort Algorithm In this tutorial, you will learn about the quick sort algorithm and its implementation in Python, Java, C, and C++. Quicksort is a sorting algorithm based on the divide and conquer approach where An array is divided into subarrays by se
www.programiz.com